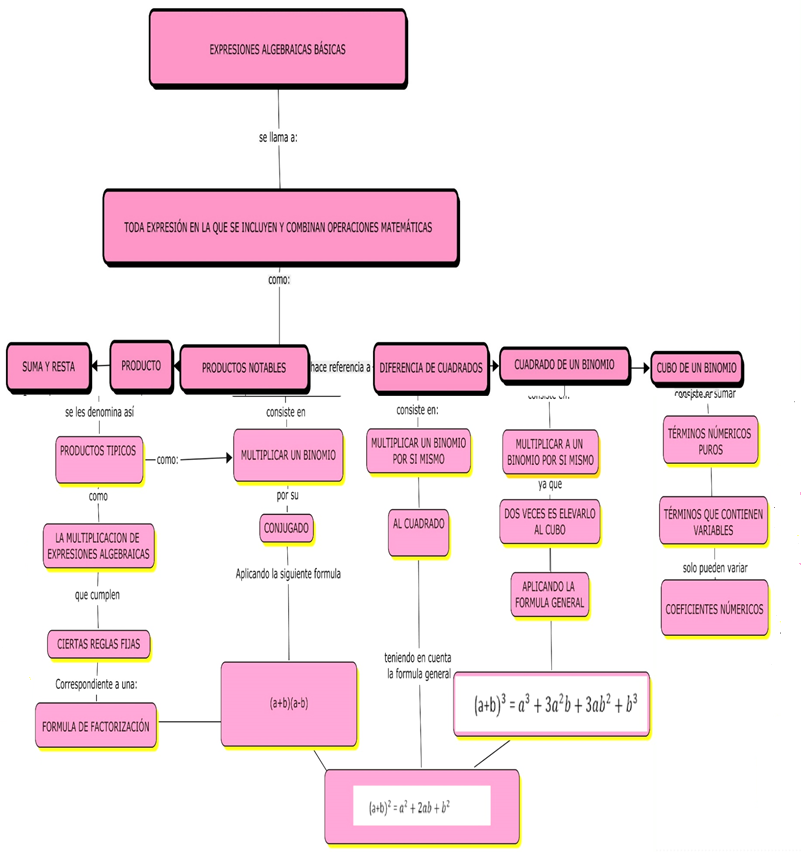
EXPRESIONES ALGEBRAICAS
Se llama así toda expresión en la que se incluyen y
cambian de cualquier forma: operaciones matemáticas, número y variables
o partes literales (estas variables son las que se expresan
simplemente con una variable) un ejemplo muy claro son los siguientes:
- 2x+1
- 5(x+3) 2+3ª
Teniendo en cuenta las
operaciones básicas, ya que así como se puede operar con números, también se
puede hacer con expresiones algebraicas.
En primer lugar encontramos
la suma y la resta donde se deben
tener en cuenta las siguientes reglas:
- Se puede sumar o restar entre si los términos numéricos puros de ambas expresiones
- Se puede sumar o restar entre si los términos que contienen variables, solo cuando la parte literal de ambos términos es exactamente igual, solo puede variar sus coeficientes numéricos.
En este mismo orden de
ideas encontramos producto de
expresiones algebraicas, donde se aplica los productos de binomio que se
refiere a una única variable y/o a un término numérico puro, teniendo en cuenta
la aplicabilidad de la propiedad distributiva con respecto a la suma o a la
resta.
Ejemplo: (3x). (x-4).
DIFERENCIA
DE CUADRADO:
Consiste básicamente en multiplicar un binomio por su conjugado, donde el
conjugado del binomio es el mismo binomio con el segundo término cambiando de
signo, utilizando la siguiente formula:
Esta fórmula nos sirve para ahorrar tiempo, cuando tenemos
que hacer un producto de un binomio por su conjugado, ya que en lugar de hacer
la distributiva, nos ahorramos unos puntos si aplicamos esta fórmula.
CUADRADO
DE UN BINOMIO: consiste en multiplicar un
binomio por si mismo es elevarlo al cuadrado aplicando la siguiente fórmula:
Es la formula general que
usaremos cuando queramos elevar un binomio al cuadrado.
Esta es la fórmula general
que usaremos cuando queramos elevar un binomio al cubo, la cual significa
elevar el primer término al cubo, más el triple del primer término al cuadrado
por el segundo. Mas el triple del primer término por el segundo al cuadrado y
más el segundo término elevado al cubo.
BIBLIOGRAFIA: Expresiones algebraicas básicas. Extraído el 12 de agosto del 2014 de: http://datateca.unad.edu.co/contenidos/551108/Algebra_Trigonometria_y_Geometria_Analitica_2014_-_2/Tema_33.pdf



No hay comentarios:
Publicar un comentario